Su-Schrieffer-Heeger (SSH) model
SSH Hamiltonian
SSH 模型:带有交错电子跃迁强度的双原子链,如下图所示:

只考虑电子跃迁而忽略电子电子相互作用,紧束缚模型给出的Hamiltonian如下:
其中
一维链模型总带边界,但我们更关心体(bulk)的性质,如在热力学极限系统的性质总是与边界条件选取无关。取周期性边界条件,bulk Hamiltonian为:
薛定谔方程为:
为了求解bulk的本征波函数,我们利用Bloch定理,对位置
其中
我们引入bulk动量空间哈密顿量
坐标空间的晶格平移对称性在动量空间表现为:
不难求得
其能量本征值为:
色散关系图为:
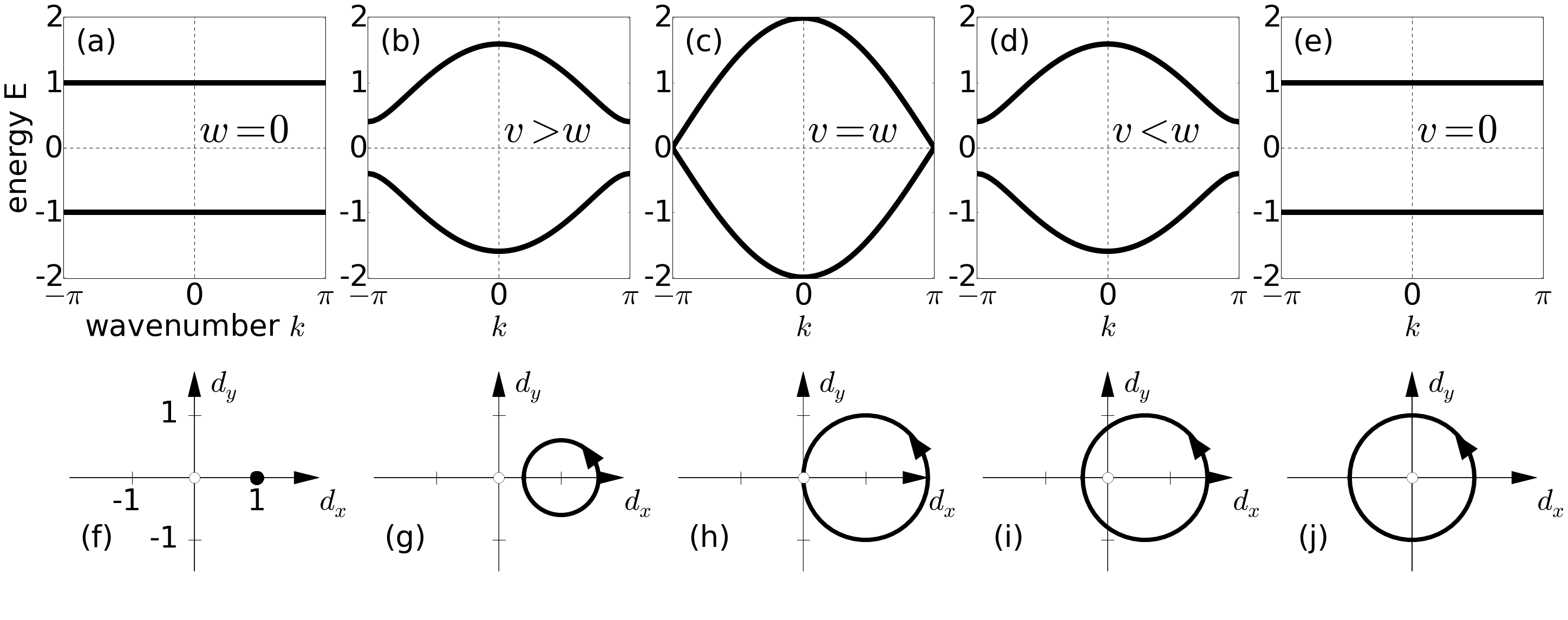
可以看出
能隙为
拓扑相
其中
则本征函数利用二分量旋量表示为:
相应的Berry联络为:
利用Berry联络的积分Berry相位可以区分色散关系
- 平凡绝缘体
- 拓扑绝缘体
- 拓扑相:由于Berry相在绝热变化下不变,我们可以根据绝热变化下能否互相转化的态进行相分类,此时Berry相起到一个序参量的作用(注意:Berry相并非局域的,这也是拓扑相区别于传统相的特征之一)。
由此我们可以给出SSH model的相图:
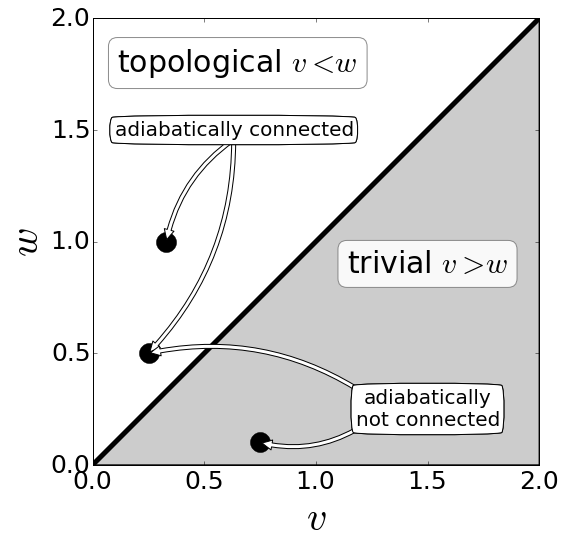
- 缠绕数:由于Berry phase反映的是SSH model 到磁场(
手征对称性与边缘态
手征对称性
手征对称性要求
- 如果手征对称性存在,由于
- 如果手征对称性破缺

因此我们称缠绕数受手征对称性保护。
- 边缘态: 尽管我们主要关心bulk的性质,但在拓扑非平凡时边缘态实际上零能构成费米面,具有一些奇特的性质。
研究边缘态最简单的情形是考虑二聚物极限,即取

如果逐步取消二聚物极限:
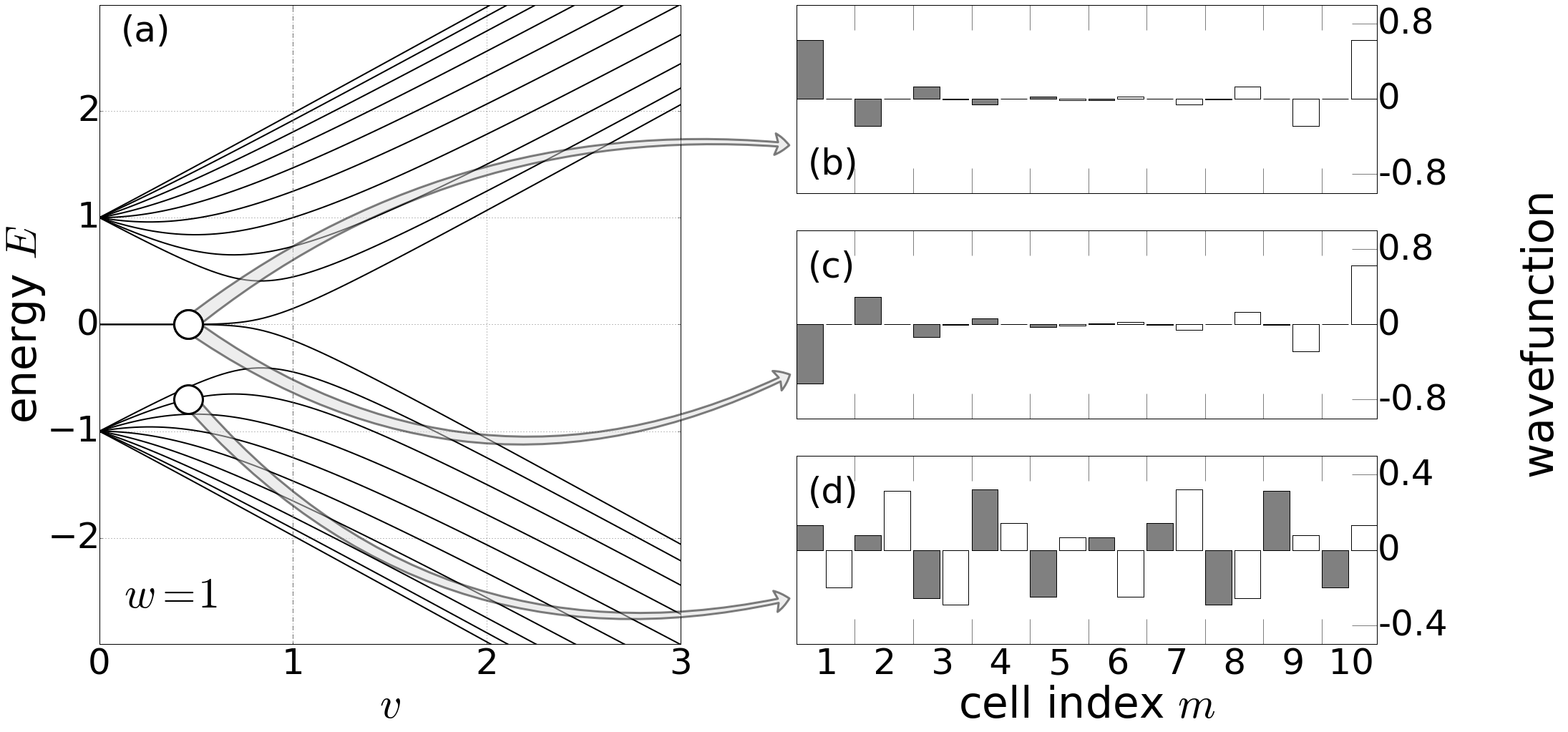
可以看出在
- 体边对应:
事实上边缘态的数目